|
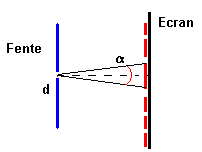
2-Diffraction Lorsqu'un rayon lumineux rencontre une ouverture fine, la lumière ne se propage
plus en ligne droite. Elle est diffractée par la fente dans un plan perpendiculaire.
On obtient sur l'écran une série de taches lumineuses avec une tache centrale brillante
de diamètre angulaire angulaire a. |
| 3-Figures de diffraction par une fente ou par une
ouverture circulaire. |
 |
diamètre
angulaire de la tache centrale : a = 2*l/d
a diamètre angulaire en radian
d largueur de la fente en mètre
l longueur d'onde en mètre |

|
diamètre
angulaire de la tache centrale : a = 2.44*l/d
d diamètre de l'ouverture ciculaire en mètre |
|
4-Diamètre angulaire

|
Le diamètre angulaire a est
l'angle sous lequel on voit un objet à une distance donnée.
Les angles se mesurent :
*en radian,
*degré( 180° = Pi radian)
*minute d'arc (1° = 60 minute)
*en seconde d'arc (1' = 60 seconde d'arc).. |

|
*30 minute
d'arc 0.5 degré est l'angle sous lequel on voit la Lune depuis la terre.
*1 minute d'arc est l'angle sous lequel on verrait un homme
situé à 6km si l'oeil était assez puissant ou une pièce de 5f à 70m.
*1 seconde d'arc est l'angle sous lequel on verrait un homme
situé à 360 km si l'oeil était assez puissant
|

|
*0.001 seconde
d'arc est est l'angle sous lequel on verrait un homme situé sur la Lune depuis la
terre si l'oeil était assez puissant. |
|
 Fresnel
Fresnel